1. Residually Finite Groups

Posted on April 2, 2014 by sballas

Let \Sigma be a surface and let \Gamma=\pi_1(\Sigma).

Question: How many finite homomorphic images of \Gamma are there (up to isomorphism)?

We will show in a precise sense that the answer to this question is lots!

Before proceeding we see how this question is related to a lifting problem in topology. Let \alpha be a homotopically non-trivial curve on \Sigma.

Question: Is it possible to promote \alpha to an embedding in a finite sheeted cover?

Lets look at the following example.

Lifting the immersed loop \alpha to an embedded loop \tilde \alpha in a doubl

The curve \alpha is not embedded in \Sigma, but if we pass to a double cover \Sigma' we see that \alpha has a lift \tilde\alpha that is embedded. Let’s rephrase this topological lifting problem in terms of group theory.

Recall from covering space theory that \Gamma acts properly discontinuously and freely on the universal cover \tilde\Sigma of \Sigma. Let \alpha be a loop in \Sigma. The loop \alpha is compact and we can choose a path \tilde\alpha in \tilde\Sigma that lifts \alpha. This lift is also compact and so by proper discontinuity of the action we see that the set

S=\{\gamma\in \Gamma\vert \gamma\cdot \tilde\alpha\cap \tilde\alpha\neq\emptyset\}

is finite. We also see that \alpha is embedded in \Sigma if and only if S=\{e\}. Therefore, if we can find a finite index subgroup H\leq \Gamma such that S\cap H=\{e\} then \alpha will lift to an embedding in the finite sheeted cover \Sigma'=\tilde\Sigma/H. This tells us that our topological lifting problem will be solved for arbitrary \alpha if given a finite set of prescribed non-identity elements of \Gamma we can always find a finite index subgroup H\leq \Gamma that avoids this finite set. Furthermore, it suffices to exclude the elements one at a time. To see this observe that if \{\gamma_1,\ldots,\gamma_n\} is a finite set of non-identity elements and H_i is a finite index subgroup such that \gamma_i\notin H_i then \cap_iH_i is a finite index subgroup that avoids the set \{\gamma_1,\ldots,\gamma_n\}.

This motivates the following group theoretic definition.

Definition: Let G be a finitely generated (f.g.) group. Then G is residually finite (RF) if for every e\neq \gamma\in G there exists a finite index subgroup H\leq G such that \gamma\notin H.

Our previous discussion shows that if \Gamma is RF then we will be able to solve our lifting problem for arbitrary \alpha\subset \Sigma.

The following theorem gives a few alternate characterizations of RF that will be useful for us.

Theorem 1.1: Let G be a f.g. group, then the following are equivalent

  1. G is RF
  2. If e\neq \gamma\in G then \exists H\leq G of finite index such that \gamma\notin H
  3. If e\neq \gamma\in G then \exists K\unlhd G of finite index such that \gamma\notin K
  4. \bigcap_{H\stackrel{f.i.}{\leq}G}H=\{e\}

proof: 1\Leftrightarrow 2 follows from the definition and 2\Leftrightarrow 4 and 3\Rightarrow 2 are obvious. That leaves 2\Rightarrow 3. Let e\neq \gamma\in G and let H\stackrel{f.i.}{\leq}G such that \gamma\notin H. Let n=[G:H], then there is an action of G on the set of left cosets of H in G. This induces a homomorphism f:G\to S_n where S_n is the symmetric group on n letters. Let K be the kernel of this homomorphism, then K\stackrel{f.i.}{\unlhd}G. Since K\leq H we see that \gamma \notin K. \Box

Remark: As a result of Theorem 1.1 we see that non-identity elements of residually finite groups can be distinguished from the identity in finite quotients.

The following lemma tells us how RF behaves when passing to subgroups and supergroups of finite index.

Lemma 1.2: Let G be a f.g. group

  1. If G is RF and H\leq G then H is RF
  2. If G is RF and G\stackrel{f.i.}{\leq}H then H is RF.

proof: Let e\neq g\in H then we can find a homomorphism f:G\to F where F is a finite group such that f(g)\neq e_F. We can restrict f to a homomorphism f':H\to F and we let K=\ker f'. By construction K is a finite index normal subgroup of H such that g\notin K. Thus H is RF.

Let e\neq g\in H. There are two cases. If g\notin G then we have excluded g from a finite index subgroup of $\latex H$. If g\in G then we can find a finite index subgroup L\leq G such that g\notin L. Since L\stackrel{f.i.}{\leq}G\stackrel{f.i.}{\leq}H we see that L\stackrel{f.i.}{\leq}H and so we have excluded g from a finite index subgroup of H.\Box

We can now begin to show that surface groups are RF. From now on we will assume that all surfaces are of finite type (finite genus with finitely many boundary components). Let \Sigma_{g,n} be the surface with genus g and n boundary components. We will denote \Sigma_{g,0} as \Sigma_g.

Exercise: If \chi(\Sigma)\geq 0 then prove that \pi_1(\Sigma) is RF.

The following two lemmas help reduce the proof that fundamental groups of surfaces are RF to finitely many cases.

Lemma 1.3: Let g\geq 2 then \Sigma_g is a finite sheeted cover of \Sigma_2.

proof: As we saw in class, we draw \Sigma_g as a “pin wheel with g-1 spokes.” With this perspective it is easy to see that \Sigma_g admits a fixed point free self homeomorphism f of order g-1 given by rotating the pin wheel. We can realize \Sigma_2 as \Sigma_g/\langle f\rangle and the induced quotient map is easily seen to be a covering map. \Box

Combining this with Lemma 1.2 we see that if we can show that \pi_1(\Sigma_2) is RF then we will know that all closed surfaces have residually finite fundamental groups.

Remark: It is a basic fact from algebraic topology that non-closed surfaces have free fundamental groups and in particular that if \Sigma is non-closed with negative Euler characteristic then its fundamental group is not Abelian.

Lemma: Let n\geq 2 then F_n is a finite index subgroup of F_2 of index n-1.

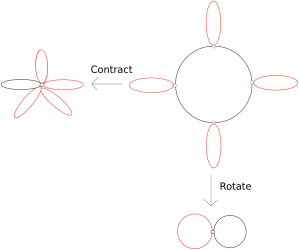
proof: From algebraic topology we know that the fundamental group of a rose with n petals is F_n. Take a “pin wheel graph with n-1 spokes.” If we quotient by a graph automorphism of order n-1 given by rotating then we get an n-1 sheeted covering of the rose with 2 petals by this pinwheel graph. If we contract a maximal tree in the pinwheel graph we get a rose with n petals. The figure below demonstrates the case when n=5.

rose

Since this contraction is a deformation retract we have not changed the fundamental group and so the pinwheel has F_n as its fundamental group. Thus F_n is an index n-1 subgroup of F_2. \Box

Remark: The ideas in the proof of Lemma 1.4 are the basis of an easy topological proof of the fact that all subgroups of a free group are free.

As a result we see that if we can show that F_2 is RF then all non-closed surface groups will be residually finite.

This entry was posted in Uncategorized and tagged , . Bookmark the permalink.

1 Response to 1. Residually Finite Groups

  1. sballas says:
    April 16, 2014 at 7:49 am

    I would like to thank Nathan for bringing to my attention that my original picture of the lifting of \alpha was incorrect. I have replaced it with a (hopefully) correct version.

    Reply

Leave a comment